数据结构
线性数据结构
线性数据结构是一个有序数据元素的集合,其中数据元素之间的关系是一对一的关系。 常见的线性结构有:线性表,栈,队列,数组等。
线性表
线性表(list)是最基本的数据结构,它是由零个或多个数据元素组成的有序集合, 这个有序不是指的排序后的有序,而是指添加元素的顺序,假如2在1之前被放入了集合中,那么2肯定在1前面,不会因为大小原因而 改变他们在集合中的顺序。
链表的实现方式主要有数组和链表。
数组实现的线性表,访问速度是其最大的优点,但由于数组的容量是固定的,所以如果采用数组作为线性表的实现, 那么就涉及到扩容,调整元素位置等问题,这些操作是非常消耗性能的,因此数组实现的线性表适用于读多写少的环境。
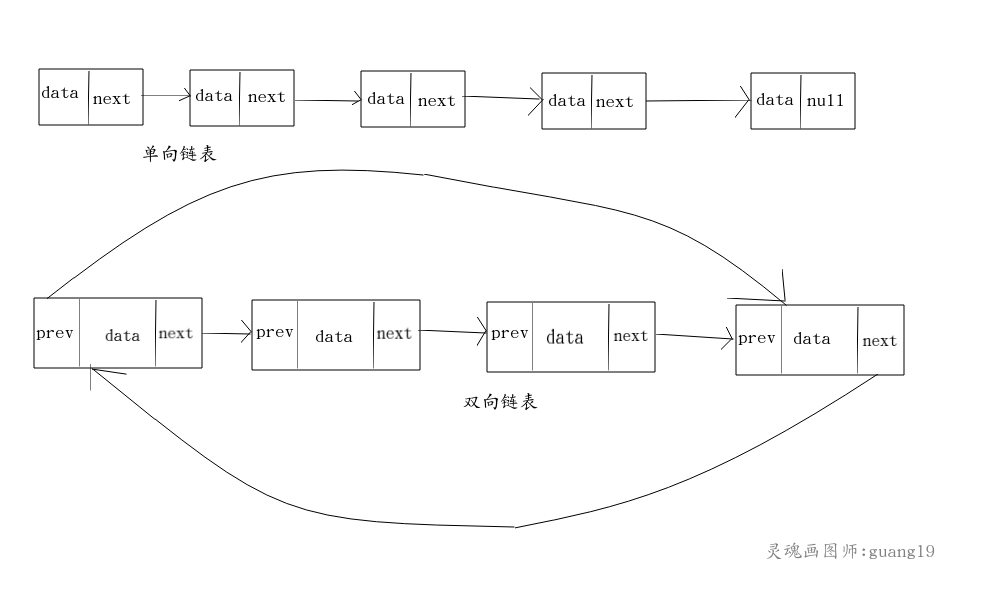
链表可以分单向链表,双端链表和双向链表(双向循环链表)。 单向链表的每个节点都保存了指向下一个节点的引用(称为next),单向链表的尾节点的下一个节点 的引用为null。
双端链表的每个Node都保存了前后2个节点的引用,双端链表的first节点的前一个节点为null, last节点的后一个节点为null。
双向链表的每个Node都保存了前后2个节点的引用, 双向链表的first节点的前一个节点指向last节点, last节点的最后一个节点指向first节点。
无论是单链表和双链表,因为每个节点都保存了其他节点的引用,所以是比较消耗内存的。
链表实现的线性表,增删改操作的性能是其最大的优点,但链表并不支持下标这种RandomAccess随机访问的方式, 所以链表实现的线性表适用于写多读少的环境。
线性表实现源码(链式队列使用的是双端链表实现的):
队列
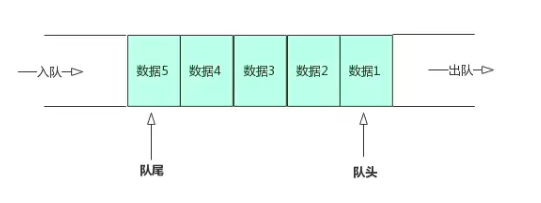
队列(queue)是一种采用先进先出(FIFO)策略的抽象数据结构,即最先进队列的数据元素, 同样要最先出队列。队列跟我们排队买票一样,先来排队的肯定先买票,后来排队的的后买到票。
队列有两个重要的概念,一个叫队首,一个叫队尾,队首指向的是第一个元素,而队尾指向的是最后一个元素。 队列有两个主要的操作:入队(enqueue)操作 和 出队(dequeue)。 入队操作是将一个元素添加到队尾,出队操作就是取出队首的元素。
队列的底层可以用数组和链表实现。
对于数组实现的队列来说,其容量肯定是有限制的,当队列满了之后,如何能够再次使用呢? 这就是循环队列的作用了。
队列实现源码:
PS:关于队列,可以参考: 掘金 - 队列 , 写得很详细。
栈
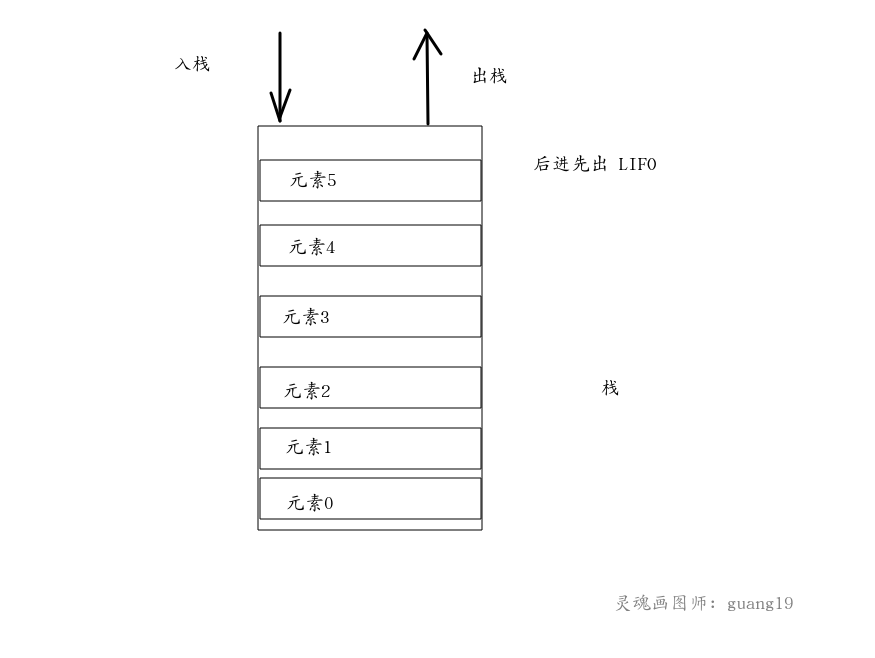
栈(stack)是一种后进先出(LIFO)的数据结构,即最后进入栈中的元素,最先出栈。 栈有两个主要的操作: 入栈(push) 和 出栈(pop)。 入栈操作是将一个元素置于栈顶,出栈操作是将栈顶元素取出。
栈同样可以由数组和链表实现,对于数组实现的栈来说,其容量肯定也有限制,所以个人认为实现栈的较好的方式是链表。
栈实现源码:栈
非线性数据结构
非线性数据结构中各个数据元素不再保持在一个线性序列中,每个数据元素可能与零个或者多个其他数据元素发生联系。 根据关系的不同,可分为层次结构和群结构。
常见的非线性数据结构主要有矩阵(多维数组),广义表,树,图等。
稀疏数组
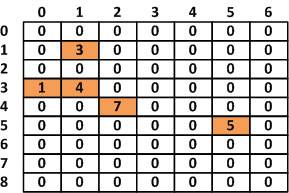
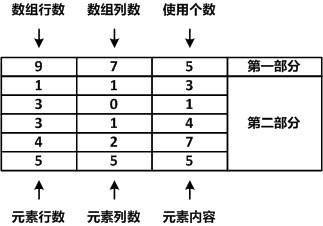
稀疏数组又被称为稀疏矩阵,它本质上是一个二维数组。 当一个数组中大部分元素都未被使用,仅有少部分被占用,这就造成了空间的浪费。 为了解决这种问题,可以使用稀疏数组来保存该数组的数据,稀疏数组可以理解为原数组被压缩后的数组。
如图所示,有大部分的空间是无用的:
我们使用稀疏数组进行压缩,稀疏数组的第一部分所记录的是原数组的行数和列数,即元数据。 第二部分记录原数组中的有效值的位置和值。这样经过压缩后的数组不再需要分配原数组那么大的空间,解决了空间浪费的问题。
稀疏数组源码: 稀疏数组
Hash表
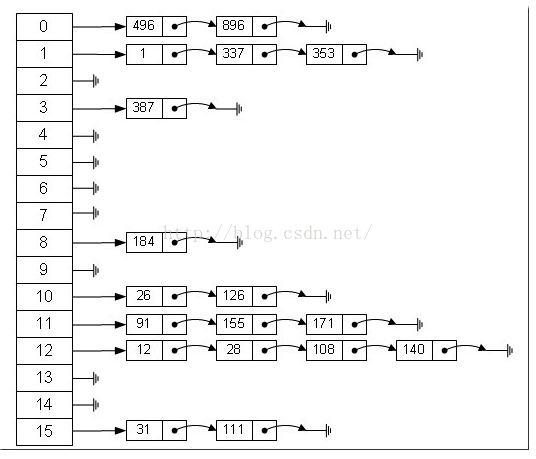
Hash表是一种能够快速访问,快速删除与修改的数据结构。我们知道数组的访问速度非常快,链表的增删改等操作的效率也是 非常高的,那有没有一种数据结构能够融合数组和链表的优点呢?可以说Hash表就是这样一种数据结构。
Hash表是通过关键码(key)进行访问,通过Hash表存储数据的数据结构,它通过某种映射函数将关键码映射到 Hash表的某个位置从而进行快速定位。 其中映射函数被称为散列函数(Hash函数),Hash表被称为散列表。
Hash表源码: HashTable
树
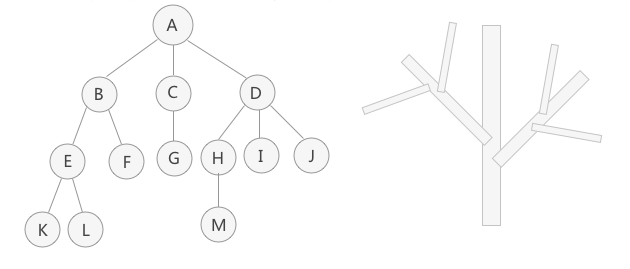
树是一种抽象的数据类型,它是由n个有限节点组成的一个具有层次关系的集合,因其结构像一棵倒状的树,所以称其为树结构。
树的重要的概念
节点(结点): 在树结构中,存储数据的每个元素都被称为节点,如上图中的A,B,C等都是节点。
父节点: 一个节点A如果包含了另一个节点B, 则节点A就是节点B的父节点,节点B是节点A的子节点。
兄弟节点: 若多个节点具有相同的父节点,这些节点就是兄弟节点。
根节点: 每棵非空的树都有且仅有一个根节点,上图的A就是根节点。
叶子节点: 如果一个节点没有任何子节点,那么此节点就是叶子节点,上图的K,L,F,G等都是叶子节点。
节点的度: 节点的度是指该节点拥有的子树数。
树的度: 一棵树中,最大的节点度就是这棵树的度。
树的深度: 从这个树的根节点出发,根节点处于第一层,其孩子节点处于第二层,依次往下。上图树的深度 为4或3(计算方法的不同而已,如果把根节点算作第0层,那么树的深度就是3)。
森林: 由m棵互不相交的树组成的集合被称为森林,上图中,以B,C,D为根节点的三棵子树就组成了森林。
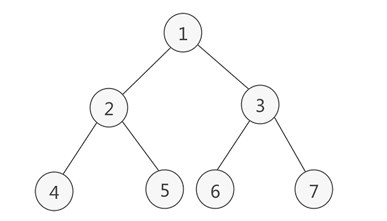
二叉树
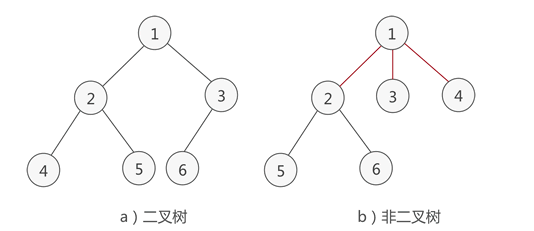
二叉树是一种特殊的树结构,二叉树的每个节点最多有2棵子树,即二叉树的节点的度最大为2。
二叉树主要有如下性质:
二叉树的第 i 层最多有 2^(i-1) 个节点。
如果二叉树的为 d,那么二叉树总共有不超过 (2^d)-1 个节点。
二叉树有许多不同的种类,如: 满二叉树,完全二叉树,排序二叉树(二叉搜索树,二插查找树),平衡二叉树等。
和线性表一样,二叉树也有链表(节点)实现和数组实现,数组实现的二叉树被称为 顺序存储的二叉树。
二叉树实现:
满二叉树
满二叉树除了叶子节点,其他的节点的子树都为2,即除了叶子节点外, 它的每个节点的度都为2。
满二叉树主要有如下性质:
满二叉树的第 i 层的节点有 2(i-1) 个。
满二叉树的深度为 d , 那么此满二叉树必须有: (2^d)-1 个节点。
具有 n 个节点的满二叉树的深度为: log2(n+1)。
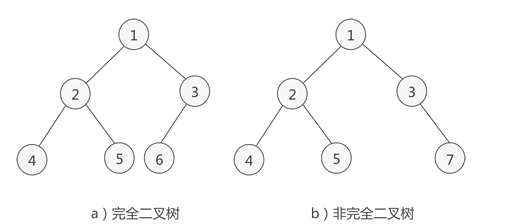
完全二叉树
如果一棵二叉树除去最后一层节点外是满二叉树,且最后一层节点是从左到右紧密分布的,那么此二叉树是一棵 完全二叉树。
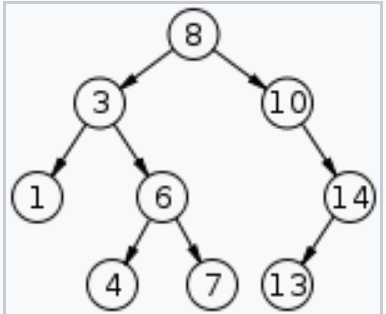
二叉查找树(BST)
二叉查找树(Binary Search Tree)也被称为为二插排序树(Binary Sort Tree)。 二叉排序树具有如下性质:
若根节点的左子树不为空,那么其左子树的所有节点的值必将小于根节点的值。
若根节点的右子树不为空,那么其右子树的所有节点的值必将小于根节点的值。
左右子树也都是二叉查找树。
BST的左子节点的值小于根节点的值小于右子节点的值,这代表着如果对一棵BST进行中序遍历,那么即可得到 一个有序的数列。
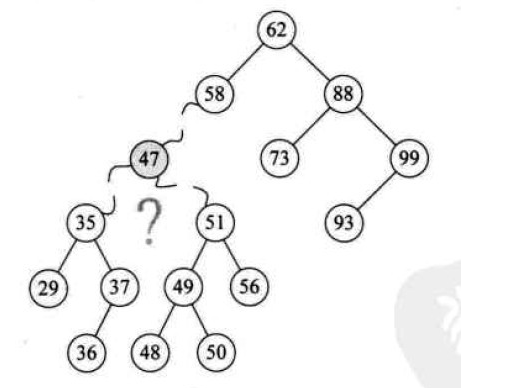
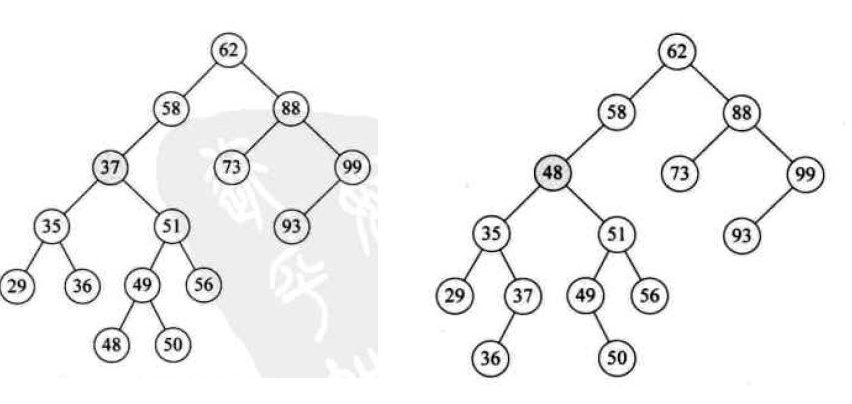
关于BST的操作,我觉得这里需要讲解一下他的删除操作。 BST的删除操作的节点需要分为三种情况,这里只探讨: 要删除的节点既有左子树也有右子树的情况。 当BST需要执行删除操作的时候,如果要删除的节点既有左子节点,也有右子节点,那么就需要找到这个节点的 前驱节点或者后继节点,然后使用前驱节点或后继节点替换掉要删除的节点,这里的前驱节点和后继节点并不是指 前一个或下一个,而是指按二叉树的中序遍历顺序来讲,遍历这个节点时,它的前一个节点和后一个节点。
如下图,要删除的节点为 47:
那么当中序遍历此BST时,47的前驱节点为37,后继节点为48,当使用前驱节点或后继节点替换掉要删除的节点后, 那么会有如下2种结果:
至于使用前驱还是后继,这个可以自行选择。
二叉查找树实现: BinarySearchTree